6. Validation
Let’s go through an end-to-end process in training and validating a classification model. After understanding this process, you may modify it for your own purpose. In general, the steps are as follows.
Data: you need to acquire your data relevant to the problem and goal you are trying to achieve; here we generate synthetic data.
Missingness: typically, there is missing data and we need to figure a way to resolve this issue; here, we randomly force data to be missing at random.
Splitting: when we train a model, we desire for the model to be able to
generalizeinto the future againstunseendata; here, we split the data into training and validation sets, where the modeling pipeline will only see the training data and will be tested for performance against the unseen validation set.Training: the training pipeline is dependent on the nature and properties of your data; here, our pipeline is one-hot encoding, imputation, scaling and finally, training a model.
Validation: after we done training a model, we cross-validate the model against unseen data; here, the unseen data is the holdout validation set.
6.1. Generate data
Below, we simulate data D.
\(X_1 \sim \mathcal{N}(0, 1)\)
\(X_2 \sim \mathcal{N}(0, 1)\)
\(X_3\) is
redwhen \(X_1 < 0\) and \(X_2 < 0\)greenwhen \(X_1 > 0\) and \(X_2 > 0\)blueotherwise
\(Y_0 = 1 + 2X_1 + 3X_2 + \sigma\)
\(Y_1 = \frac{1}{1 + \exp(-Y_0)}\)
\(y \sim \mathcal{Binom}(Y_1)\)
[1]:
suppressMessages({
library('dplyr')
library('purrr')
})
set.seed(37)
getColor <- function(a, b) {
if (a < 0 && b < 0) {
return('red')
} else if (a > 0 && b > 0) {
return('green')
} else {
return('blue')
}
}
getData <- function(N=1000) {
x1 <- rnorm(N, mean=0, sd=1)
x2 <- rnorm(N, mean=0, sd=1)
x3 <- map2(x1, x2, getColor) %>% flatten_chr()
y <- 1 + 2.0 * x1 + 3.0 * x2 + rnorm(N, mean=0, sd=1)
y <- 1.0 / (1.0 + exp(-y))
y <- rbinom(n=N, size=1, prob=y)
df <- data.frame(x1=x1, x2=x2, x3=x3, y=y)
df <- df %>%
mutate(y=ifelse(y == 0, 'neg', 'pos')) %>%
mutate_at('y', as.factor)
return(df)
}
D <- getData()
[2]:
print(sapply(D, is.factor))
x1 x2 x3 y
FALSE FALSE TRUE TRUE
[3]:
print(head(D))
x1 x2 x3 y
1 0.1247540 0.4817417 green pos
2 0.3820746 0.8176848 green pos
3 0.5792428 -0.3254274 blue pos
4 -0.2937481 -0.2674061 red pos
5 -0.8283492 1.7163252 blue pos
6 -0.3327136 1.2376945 blue pos
[4]:
print(summary(D))
x1 x2 x3 y
Min. :-2.8613 Min. :-3.28763 blue :502 neg:394
1st Qu.:-0.6961 1st Qu.:-0.59550 green:257 pos:606
Median :-0.0339 Median : 0.06348 red :241
Mean :-0.0184 Mean : 0.03492
3rd Qu.: 0.6836 3rd Qu.: 0.69935
Max. : 3.8147 Max. : 3.17901
[5]:
print(dim(D))
[1] 1000 4
6.2. Generate missing data
Here, we make 10% of the data missing in D and store the results in D.M.
[6]:
suppressMessages({
library('missForest')
})
D.M <- prodNA(D[c('x1', 'x2', 'x3')], noNA=0.1)
D.M$y <- D$y
[7]:
print(summary(D.M))
x1 x2 x3 y
Min. :-2.86131 Min. :-3.28763 blue :457 neg:394
1st Qu.:-0.70096 1st Qu.:-0.61616 green:225 pos:606
Median :-0.02752 Median : 0.06288 red :213
Mean :-0.03416 Mean : 0.03213 NA's :105
3rd Qu.: 0.65422 3rd Qu.: 0.69815
Max. : 3.81473 Max. : 3.17901
NA's :102 NA's :93
[8]:
print(dim(D))
[1] 1000 4
6.3. Split data
Now we split D.M into 80% training D.T and 20% testing D.V.
[9]:
suppressMessages({
library('caret')
})
trIndices <- createDataPartition(D$y, times=1, p=0.8, list=FALSE)
D.T <- D.M[trIndices, ]
D.V <- D.M[-trIndices, ]
[10]:
print(head(D.T))
x1 x2 x3 y
1 0.1247540 0.4817417 green pos
2 0.3820746 0.8176848 green pos
3 0.5792428 -0.3254274 blue pos
5 NA 1.7163252 blue pos
7 -0.1921595 -1.1223299 red neg
8 1.3629827 1.5202646 <NA> pos
[11]:
print(head(D.V))
x1 x2 x3 y
4 -0.2937481 -0.2674061 red pos
6 -0.3327136 1.2376945 blue pos
26 -0.4590474 1.5723978 blue pos
29 -2.1039691 1.0775911 blue pos
33 0.6553955 NA blue neg
36 0.1297151 0.2434078 green pos
[12]:
print(dim(D.T))
[1] 801 4
[13]:
print(dim(D.V))
[1] 199 4
6.4. Profile data
6.4.1. Statistical profiles
Now, let’s quickly look at the data profiles.
6.4.1.1. Training profile
[14]:
library('skimr')
skimmed <- skim(D.T[,1:2])
s <- skimmed[, c(2:6, 12)]
print(s)
# A tibble: 2 x 6
skim_variable n_missing complete_rate numeric.mean numeric.sd numeric.hist
<chr> <int> <dbl> <dbl> <dbl> <chr>
1 x1 87 0.891 -0.0156 0.994 ▁▅▇▃▁
2 x2 73 0.909 0.0337 1.04 ▁▃▇▅▁
[15]:
skimmed <- skim(D.T[,3:4])
s <- skimmed[, c(2:7)]
print(s)
# A tibble: 2 x 6
skim_variable n_missing complete_rate factor.ordered factor.n_unique
<chr> <int> <dbl> <lgl> <int>
1 x3 81 0.899 FALSE 3
2 y 0 1 FALSE 2
# … with 1 more variable: factor.top_counts <chr>
6.4.1.2. Validation profile
[16]:
skimmed <- skim(D.V[,1:2])
s <- skimmed[, c(2:6, 12)]
print(s)
# A tibble: 2 x 6
skim_variable n_missing complete_rate numeric.mean numeric.sd numeric.hist
<chr> <int> <dbl> <dbl> <dbl> <chr>
1 x1 15 0.925 -0.106 1.05 ▂▇▇▂▁
2 x2 20 0.899 0.0257 0.977 ▁▂▇▅▁
[17]:
skimmed <- skim(D.V[,3:4])
s <- skimmed[, c(2:7)]
print(s)
# A tibble: 2 x 6
skim_variable n_missing complete_rate factor.ordered factor.n_unique
<chr> <int> <dbl> <lgl> <int>
1 x3 24 0.879 FALSE 3
2 y 0 1 FALSE 2
# … with 1 more variable: factor.top_counts <chr>
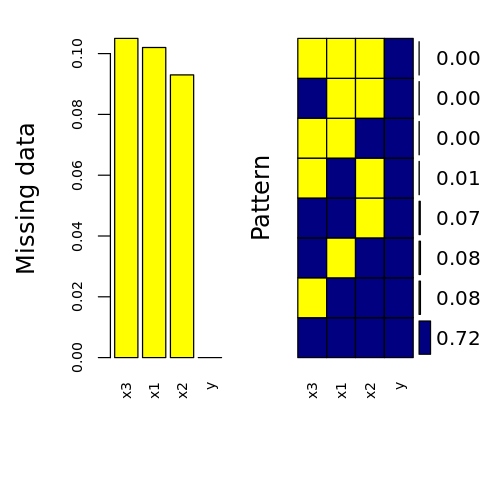
6.4.2. Missingness profiles
Below, we visually inspect the data missingness.
[18]:
suppressMessages({
library('VIM')
})
options(repr.plot.width=4, repr.plot.height=4)
p <- aggr(
D.M,
col=c('navyblue','yellow'),
numbers=TRUE,
sortVars=TRUE,
labels=names(D.M),
cex.axis=.7,
gap=3,
ylab=c('Missing data', 'Pattern')
)
Variables sorted by number of missings:
Variable Count
x3 0.105
x1 0.102
x2 0.093
y 0.000
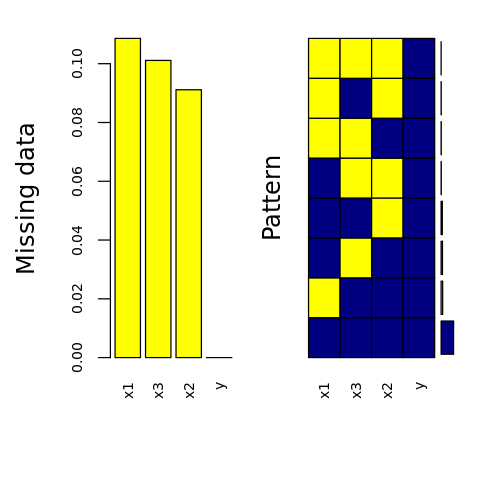
[19]:
p <- aggr(
D.T,
col=c('navyblue','yellow'),
numbers=TRUE,
sortVars=TRUE,
labels=names(D.T),
cex.axis=.7,
gap=3,
ylab=c('Missing data', 'Pattern')
)
Warning message in plot.aggr(res, ...):
“not enough horizontal space to display frequencies”
Variables sorted by number of missings:
Variable Count
x1 0.10861423
x3 0.10112360
x2 0.09113608
y 0.00000000
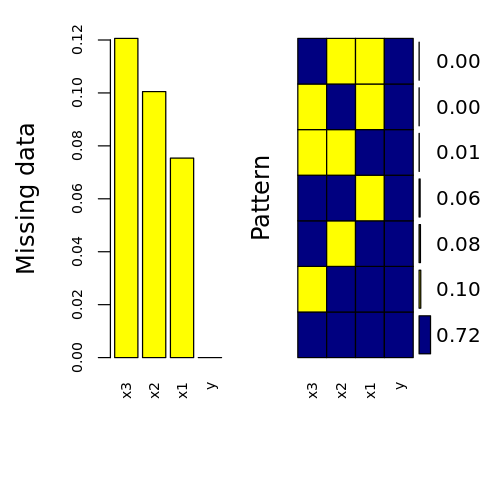
[20]:
p <- aggr(
D.V,
col=c('navyblue','yellow'),
numbers=TRUE,
sortVars=TRUE,
labels=names(D.V),
cex.axis=.7,
gap=3,
ylab=c('Missing data', 'Pattern')
)
Variables sorted by number of missings:
Variable Count
x3 0.12060302
x2 0.10050251
x1 0.07537688
y 0.00000000
6.5. One-hot encoding
We perform one-hot encoding OHE on the categorical variables and store the result in D.O. Note how we start the training pipeline at OHE? The reason is to avoid data leakage. Had we applied OHE on the whole dataset, we may bias the training process towards better results.
[21]:
ohe <- dummyVars(~ ., data=D.T[,-4], sep='_')
D.O <- data.frame(predict(ohe, newdata=D[,-4]))
D.O$y <- D$y
[22]:
print(head(D.O))
x1 x2 x3_blue x3_green x3_red y
1 0.1247540 0.4817417 0 1 0 pos
2 0.3820746 0.8176848 0 1 0 pos
3 0.5792428 -0.3254274 1 0 0 pos
4 -0.2937481 -0.2674061 0 0 1 pos
5 -0.8283492 1.7163252 1 0 0 pos
6 -0.3327136 1.2376945 1 0 0 pos
[23]:
print(summary(D.O))
x1 x2 x3_blue x3_green
Min. :-2.8613 Min. :-3.28763 Min. :0.000 Min. :0.000
1st Qu.:-0.6961 1st Qu.:-0.59550 1st Qu.:0.000 1st Qu.:0.000
Median :-0.0339 Median : 0.06348 Median :1.000 Median :0.000
Mean :-0.0184 Mean : 0.03492 Mean :0.502 Mean :0.257
3rd Qu.: 0.6836 3rd Qu.: 0.69935 3rd Qu.:1.000 3rd Qu.:1.000
Max. : 3.8147 Max. : 3.17901 Max. :1.000 Max. :1.000
x3_red y
Min. :0.000 neg:394
1st Qu.:0.000 pos:606
Median :0.000
Mean :0.241
3rd Qu.:0.000
Max. :1.000
6.6. Imputation
We will preprocess the training data using k-nearest neighbor imputation and store the result in D.I.
[24]:
library('RANN')
imp <- preProcess(D.O, method='knnImpute')
D.I <- predict(imp, newdata=D.O)
print(anyNA(D.I))
[1] FALSE
[25]:
print(head(D.I))
x1 x2 x3_blue x3_green x3_red y
1 0.1408176 0.4391669 -1.0035059 1.6994586 -0.563210 pos
2 0.3939391 0.7693556 -1.0035059 1.6994586 -0.563210 pos
3 0.5878898 -0.3541760 0.9955098 -0.5878343 -0.563210 pos
4 -0.2708553 -0.2971486 -1.0035059 -0.5878343 1.773761 pos
5 -0.7967326 1.6526029 0.9955098 -0.5878343 -0.563210 pos
6 -0.3091849 1.1821708 0.9955098 -0.5878343 -0.563210 pos
[26]:
print(summary(D.I))
x1 x2 x3_blue x3_green
Min. :-2.79652 Min. :-3.26564 Min. :-1.0035 Min. :-0.5878
1st Qu.:-0.66661 1st Qu.:-0.61962 1st Qu.:-1.0035 1st Qu.:-0.5878
Median :-0.01525 Median : 0.02807 Median : 0.9955 Median :-0.5878
Mean : 0.00000 Mean : 0.00000 Mean : 0.0000 Mean : 0.0000
3rd Qu.: 0.69053 3rd Qu.: 0.65305 3rd Qu.: 0.9955 3rd Qu.: 1.6995
Max. : 3.77058 Max. : 3.09023 Max. : 0.9955 Max. : 1.6995
x3_red y
Min. :-0.5632 neg:394
1st Qu.:-0.5632 pos:606
Median :-0.5632
Mean : 0.0000
3rd Qu.:-0.5632
Max. : 1.7738
6.7. Rescale
Let’s rescale the variables into the range [0, 1] and store the result in D.R.
[27]:
ran <- preProcess(D.I, method='range')
D.R <- predict(ran, newdata=D.I)
[28]:
print(head(D.R))
x1 x2 x3_blue x3_green x3_red y
1 0.4472809 0.5828955 0 1 0 pos
2 0.4858248 0.6348457 0 1 0 pos
3 0.5153584 0.4580750 1 0 0 pos
4 0.3845938 0.4670474 0 0 1 pos
5 0.3045163 0.7738113 1 0 0 pos
6 0.3787572 0.6997959 1 0 0 pos
[29]:
print(summary(D.R))
x1 x2 x3_blue x3_green
Min. :0.0000 Min. :0.0000 Min. :0.000 Min. :0.000
1st Qu.:0.3243 1st Qu.:0.4163 1st Qu.:0.000 1st Qu.:0.000
Median :0.4235 Median :0.5182 Median :1.000 Median :0.000
Mean :0.4258 Mean :0.5138 Mean :0.502 Mean :0.257
3rd Qu.:0.5310 3rd Qu.:0.6165 3rd Qu.:1.000 3rd Qu.:1.000
Max. :1.0000 Max. :1.0000 Max. :1.000 Max. :1.000
x3_red y
Min. :0.000 neg:394
1st Qu.:0.000 pos:606
Median :0.000
Mean :0.241
3rd Qu.:0.000
Max. :1.000
[30]:
print(dim(D.R))
[1] 1000 6
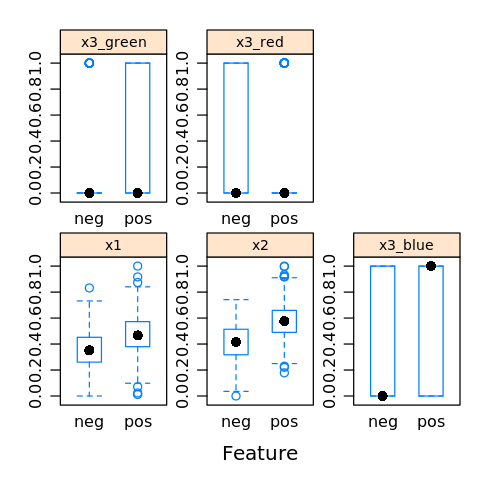
6.8. Feature importance
We may visualize feature importance to see which features/variables are important to the class variable.
[31]:
featurePlot(x=D.R[,1:5],
y=D.R$y,
plot='box',
strip=strip.custom(par.strip.text=list(cex=.7)),
scales = list(x = list(relation='free'),
y = list(relation='free')))
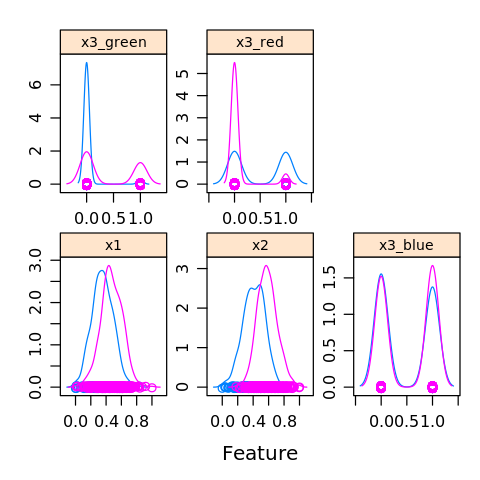
[32]:
featurePlot(x=D.R[,1:5],
y=D.R$y,
plot='density',
strip=strip.custom(par.strip.text=list(cex=.7)),
scales = list(x = list(relation='free'),
y = list(relation='free')))
6.9. Feature selection
Feature selection may help us to use only features (variables) that are important to the classification.
[33]:
ctrl <- rfeControl(
functions=rfFuncs,
method='repeatedcv',
repeats=5,
verbose=FALSE
)
profile <- rfe(y ~ ., data=D.R, sizes=c(2, 3), rfeControl=ctrl)
[34]:
profile
Recursive feature selection
Outer resampling method: Cross-Validated (10 fold, repeated 5 times)
Resampling performance over subset size:
Variables Accuracy Kappa AccuracySD KappaSD Selected
2 0.8028 0.5861 0.03459 0.07315
3 0.8102 0.5908 0.03654 0.08220
5 0.8214 0.6186 0.03640 0.08056 *
The top 5 variables (out of 5):
x2, x1, x3_red, x3_green, x3_blue
6.10. Training
We are now ready to train a classification model. We will use a random forest to classify the data. Use the modelLookup function to see which arguments are available. Below, the mtry argument/parameter is available. The model will be bound to M.
[35]:
modelLookup('rf')
| model | parameter | label | forReg | forClass | probModel |
|---|---|---|---|---|---|
| <chr> | <fct> | <fct> | <lgl> | <lgl> | <lgl> |
| rf | mtry | #Randomly Selected Predictors | TRUE | TRUE | TRUE |
[36]:
M <- train(y ~ ., data=D.R, method='rf')
[37]:
print(M)
Random Forest
1000 samples
5 predictor
2 classes: 'neg', 'pos'
No pre-processing
Resampling: Bootstrapped (25 reps)
Summary of sample sizes: 1000, 1000, 1000, 1000, 1000, 1000, ...
Resampling results across tuning parameters:
mtry Accuracy Kappa
2 0.8192793 0.6111993
3 0.8136866 0.6049471
5 0.7961271 0.5705189
Accuracy was used to select the optimal model using the largest value.
The final value used for the model was mtry = 2.
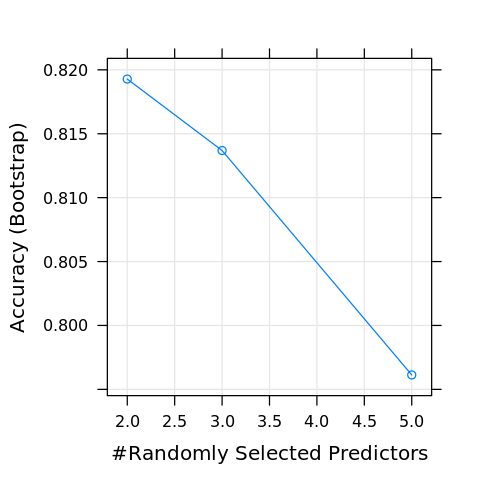
We may visualize the accuracy of the training with the predictors varying.
[38]:
plot(M)
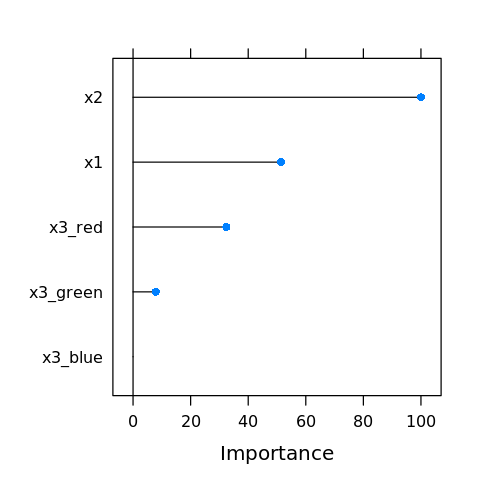
We may visualize the variable importance.
[39]:
vi <- varImp(M)
plot(vi)
6.11. Predicting on validation data
6.11.1. Transform validation data
We will not run the validation data D.V through the pipeline.
one-hot encoding,
Oimputation,
Iscaling (to the range [0, 1]),
R
[40]:
O <- predict(ohe, newdata=D.V)
[41]:
I <- predict(imp, newdata=O)
[42]:
R <- predict(ran, newdata=I)
[43]:
print(head(R))
x1 x2 x3_blue x3_green x3_red
4 0.3845938 0.4670474 0 0 1
6 0.3787572 0.6997959 1 0 0
26 0.3598337 0.7515544 1 0 0
29 0.1134421 0.6750376 1 0 0
33 0.5267653 0.4183815 1 0 0
36 0.4480240 0.5460396 0 1 0
[44]:
print(dim(R))
[1] 199 5
6.11.2. Confusion matrix
Let’s look at the confusion matrix.
[45]:
y <- predict(M, R)
cm <- confusionMatrix(reference=D.V$y, data=y, positive='pos')
[46]:
print(cm)
Confusion Matrix and Statistics
Reference
Prediction neg pos
neg 62 16
pos 16 105
Accuracy : 0.8392
95% CI : (0.7806, 0.8873)
No Information Rate : 0.608
P-Value [Acc > NIR] : 1.118e-12
Kappa : 0.6626
Mcnemar's Test P-Value : 1
Sensitivity : 0.8678
Specificity : 0.7949
Pos Pred Value : 0.8678
Neg Pred Value : 0.7949
Prevalence : 0.6080
Detection Rate : 0.5276
Detection Prevalence : 0.6080
Balanced Accuracy : 0.8313
'Positive' Class : pos
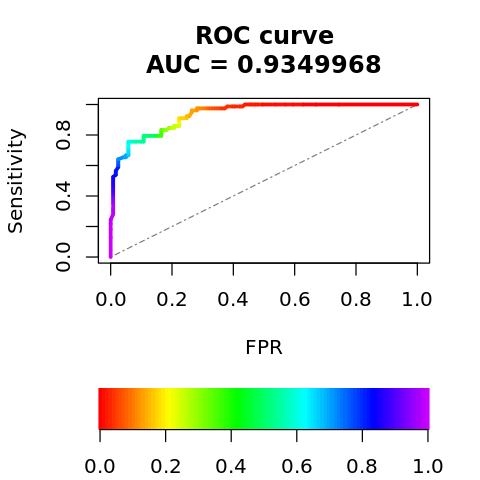
6.11.3. Receiver operating characteristic curve
Let’s look at the area under the curve (AUC) for the Receiver Operating Characteristic curve.
[47]:
library('PRROC')
y <- predict(M, R, type='prob')[,1]
results <- data.frame(
y = D.V$y,
y.pred = y
)
class.0 <- results %>% filter(y == 'neg') %>% select(y.pred)
class.1 <- results %>% filter(y == 'pos') %>% select(y.pred)
[48]:
roc <- roc.curve(
scores.class0=class.0$y.pred,
scores.class1=class.1$y.pred,
curve=TRUE,
rand.compute=TRUE)
plot(roc, legend=1, rand.plot=TRUE)
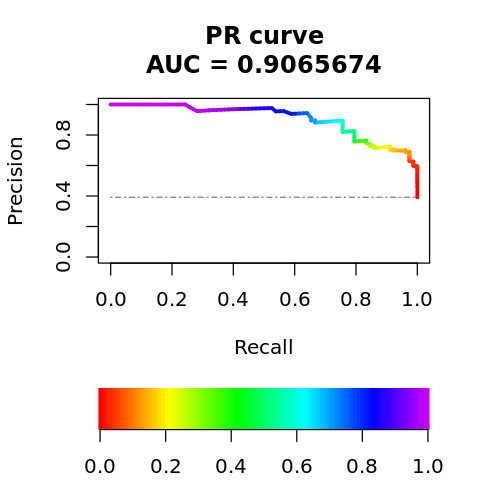
6.11.4. Precision-recall curve
The precision-recall curve is shown below.
[49]:
pr <- pr.curve(
scores.class0=class.0$y.pred,
scores.class1=class.1$y.pred,
curve=TRUE,
rand.compute=TRUE)
plot(pr, legend=1, rand.plot=TRUE)