5. Missing Data
5.1. Generate data
[1]:
set.seed(37)
suppressMessages({
library('missForest')
})
getData <- function(N=1000) {
x1 <- rnorm(N, mean=0, sd=1)
x2 <- rnorm(N, mean=0, sd=1)
y <- 5 + 3.2 * x1 - 4.2 * x2 + rnorm(N, mean=0, sd=1)
df <- data.frame(x1=x1, x2=x2, y=y)
return(df)
}
df <- getData()
df.mis <- prodNA(df, noNA=0.1)
5.2. Visualize missingness
[2]:
suppressMessages({
library('mice')
})
options(repr.plot.width=5, repr.plot.height=5)
p <- md.pattern(df.mis)
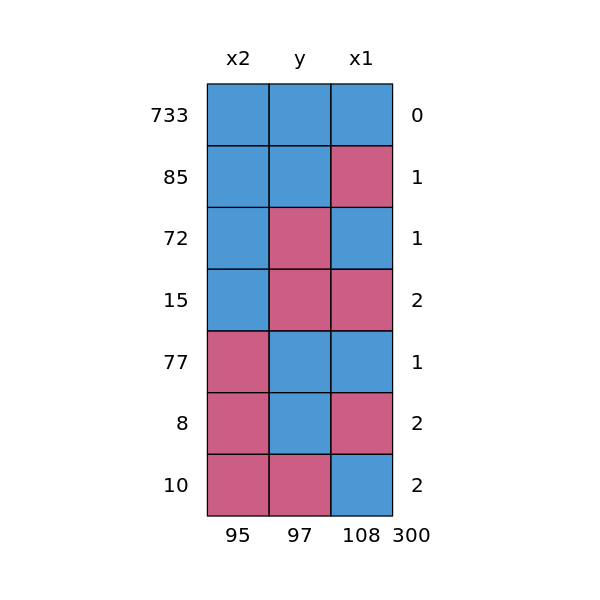
[3]:
suppressMessages({
library('VIM')
})
options(repr.plot.width=6, repr.plot.height=4)
p <- aggr(
df.mis,
col=c('navyblue','yellow'),
numbers=TRUE,
sortVars=TRUE,
labels=names(df.mis),
cex.axis=.7,
gap=3,
ylab=c('Missing data', 'Pattern')
)
Variables sorted by number of missings:
Variable Count
x1 0.108
y 0.097
x2 0.095
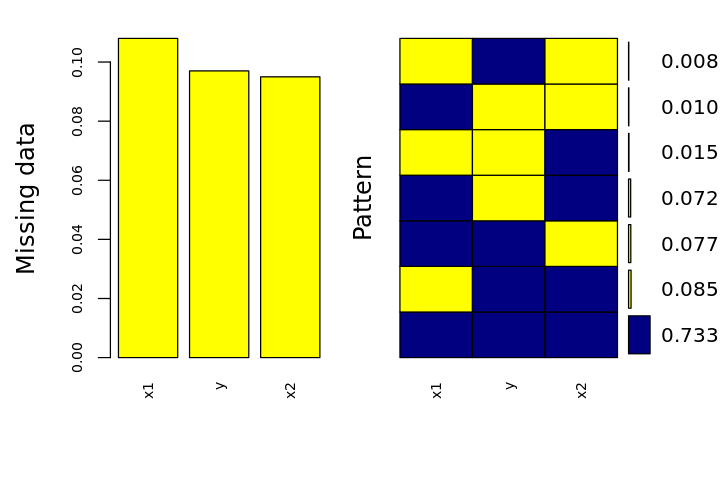
5.3. MICE
This approach imputes 5 datasets using mice.
[4]:
df.imp <- mice(df.mis, m=5, maxit=50, method='pmm', seed=500, print=FALSE)
print(summary(df.imp))
Class: mids
Number of multiple imputations: 5
Imputation methods:
x1 x2 y
"pmm" "pmm" "pmm"
PredictorMatrix:
x1 x2 y
x1 0 1 1
x2 1 0 1
y 1 1 0
NULL
[5]:
df.model <- with(data=df.imp, exp=lm(y ~ x1 + x2))
df.combine = pool(df.model)
print(summary(df.combine))
estimate std.error statistic df p.value
(Intercept) 4.978536 0.03615236 137.70984 59.17146 0
x1 3.224436 0.03845041 83.85961 28.21157 0
x2 -4.201357 0.04062838 -103.40940 21.56991 0
5.4. Amelia
Using Amelia.
[6]:
suppressMessages({
library('Amelia')
})
df.imp <- amelia(df.mis, m=5, parallel='multicore', print=FALSE)
-- Imputation 1 --
1 2 3
-- Imputation 2 --
1 2 3
-- Imputation 3 --
1 2 3
-- Imputation 4 --
1 2 3
-- Imputation 5 --
1 2 3
[7]:
m <- lm(y ~ x1 + x2, data=df.imp$imputations[[1]])
print(summary(m))
Call:
lm(formula = y ~ x1 + x2, data = df.imp$imputations[[1]])
Residuals:
Min 1Q Median 3Q Max
-2.7700 -0.6489 0.0266 0.6592 3.4818
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.01673 0.03138 159.9 <2e-16 ***
x1 3.23168 0.03058 105.7 <2e-16 ***
x2 -4.19395 0.03082 -136.1 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9918 on 997 degrees of freedom
Multiple R-squared: 0.9691, Adjusted R-squared: 0.969
F-statistic: 1.563e+04 on 2 and 997 DF, p-value: < 2.2e-16
5.5. missForest
Use missForest.
[8]:
df.imp <- missForest(df.mis, verbose=FALSE)
missForest iteration 1 in progress...done!
missForest iteration 2 in progress...done!
missForest iteration 3 in progress...done!
missForest iteration 4 in progress...done!
missForest iteration 5 in progress...done!
[9]:
m <- lm(y ~ x1 + x2, data=df.imp$ximp)
print(summary(m))
Call:
lm(formula = y ~ x1 + x2, data = df.imp$ximp)
Residuals:
Min 1Q Median 3Q Max
-3.2084 -0.5477 0.0094 0.5762 3.4938
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.99766 0.02881 173.5 <2e-16 ***
x1 3.24033 0.02854 113.5 <2e-16 ***
x2 -4.19705 0.02872 -146.1 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9104 on 997 degrees of freedom
Multiple R-squared: 0.9733, Adjusted R-squared: 0.9733
F-statistic: 1.82e+04 on 2 and 997 DF, p-value: < 2.2e-16
5.6. Hmisc
Use Hmisc.
[10]:
suppressMessages({
library('Hmisc')
})
df.imp <- aregImpute(~ x1 + x2 + y, data=df.mis, n.impute=5)
Iteration 8
[11]:
print(fit.mult.impute(y ~ x1 + x2, glm, df.imp, data=df))
Variance Inflation Factors Due to Imputation:
(Intercept) x1 x2
1.32 1.40 1.03
Rate of Missing Information:
(Intercept) x1 x2
0.24 0.29 0.03
d.f. for t-distribution for Tests of Single Coefficients:
(Intercept) x1 x2
68.07 48.58 6034.09
The following fit components were averaged over the 5 model fits:
fitted.values linear.predictors
Call: fit.mult.impute(formula = y ~ x1 + x2, fitter = glm, xtrans = df.imp,
data = df)
Coefficients:
(Intercept) x1 x2
4.986 3.224 -4.200
Degrees of Freedom: 999 Total (i.e. Null); 997 Residual
Null Deviance: 31230
Residual Deviance: 1058 AIC: 2902
5.7. mi
Impute using mi.
[12]:
suppressMessages({
library('mi')
})
df.imp <- mi(df.mis, seed=37)
[13]:
summary(df.imp)
$x1
$x1$is_missing
missing
FALSE TRUE
892 108
$x1$imputed
Min. 1st Qu. Median Mean 3rd Qu. Max.
-1.31092 -0.29634 0.05360 0.01444 0.32347 1.03555
$x1$observed
Min. 1st Qu. Median Mean 3rd Qu. Max.
-1.370380 -0.340412 -0.007915 0.000000 0.346205 1.855986
$x2
$x2$is_missing
missing
FALSE TRUE
905 95
$x2$imputed
Min. 1st Qu. Median Mean 3rd Qu. Max.
-1.16181 -0.38240 -0.09256 -0.06233 0.25807 1.45394
$x2$observed
Min. 1st Qu. Median Mean 3rd Qu. Max.
-1.63933 -0.30576 0.02156 0.00000 0.32167 1.53286
$y
$y$is_missing
missing
FALSE TRUE
903 97
$y$imputed
Min. 1st Qu. Median Mean 3rd Qu. Max.
-1.57526 -0.27385 0.07847 0.05184 0.37816 1.17524
$y$observed
Min. 1st Qu. Median Mean 3rd Qu. Max.
-1.5729109 -0.3407619 0.0007829 0.0000000 0.3281380 1.5120664